Churchill–Bernstein equation
In convective heat transfer, the Churchill–Bernstein equation is used to estimate the surface averaged Nusselt number for a cylinder in cross flow at various velocities.[1] The need for the equation arises from the inability to solve the Navier–Stokes equations in the turbulent flow regime, even for a Newtonian fluid. When the concentration and temperature profiles are independent of one another, the mass-heat transfer analogy can be employed. In the mass-heat transfer analogy, heat transfer dimensionless quantities are replaced with analogous mass transfer dimensionless quantities.
This equation is named after Stuart W. Churchill and M. Bernstein, who introduced it in 1977. This equation is also called the Churchill–Bernstein correlation.
Contents |
Heat transfer definition
![\overline{\mathrm{Nu}}_D \ = 0.3 %2B \frac{0.62\mathrm{Re}_D^{1/2}\Pr^{1/3}}{\left[1 %2B (0.4/\Pr)^{2/3} \, \right]^{1/4} \,}\bigg[1 %2B \bigg(\frac{\mathrm{Re}_D}{282000} \bigg)^{5/8}\bigg]^{4/5} \quad
\Pr\mathrm{Re}_D \ge 0.2](/2012-wikipedia_en_all_nopic_01_2012/I/01fa2369ae0e0ddbec6f69c50c91165e.png)
where:
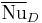 is the surface averaged Nusselt number with characteristic length of diameter;
is the surface averaged Nusselt number with characteristic length of diameter;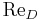 is the Reynolds number with the cylinder diameter as its characteristic length;
is the Reynolds number with the cylinder diameter as its characteristic length;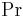 is the Prandtl number.
is the Prandtl number.
The Churchill–Bernstein equation is valid for a wide range of Reynolds numbers and Prandtl numbers, as long as the product of the two is greater than or equal to 0.2, as defined above. The Churchill–Bernstein equation can be used for any object of cylindrical geometry in which boundary layers develop freely, without constraints imposed by other surfaces. Properties of the external free stream fluid are to be evaluated at the film temperature in order to account for the variation of the fluid properties at different temperatures. One should not expect much more than 20% accuracy from the above equation due to the wide range of flow conditions that the equation encompasses. The Churchill–Bernstein equation is a correlation and cannot be derived from principles of fluid dynamics. The equation yields the surface averaged Nusselt number, which is used to determine the average convective heat transfer coefficient. Newton's law of cooling can then be invoked to determine the heat loss or gain from the object, fluid and/or surface temperatures, and the area of the object, depending on what information is known.
Mass transfer definition
![\mathrm{Sh} = 0.3 %2B \frac{0.62\mathrm{Re}_D^{1/2}\mathrm{Sc}^{1/3}}{\left[1 %2B (0.4/\mathrm{Sc})^{2/3} \, \right]^{1/4} \,}\bigg[1 %2B \bigg(\frac{\mathrm{Re}_D}{282000} \bigg)^{5/8}\bigg]^{4/5} \quad
\mathrm{Sc}\,\mathrm{Re}_D \ge 0.2](/2012-wikipedia_en_all_nopic_01_2012/I/901304b196643097f45cedd8e2dc979e.png)
where:
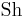 is the Sherwood number
is the Sherwood number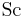 is the Schmidt number
is the Schmidt number
Using the mass-heat transfer analogy, the Nusselt number is replaced by the Sherwood number, and the Prandtl number is replaced by the Schmidt number. The same restrictions described in the heat transfer definition are applied to the mass transfer definition. The Sherwood number can be used to find an overall mass transfer coefficient and applied to Fick's law of diffusion to find concentration profiles and mass transfer fluxes.
Notes
- ^ Some examples of said system can be seen here: "Cylinder in Cross Flow at Various Velocities". Flometrics. 1997. http://www.flometrics.com/services/cylinder/cylinder.html. Retrieved 10/07/2007.
See also
References
- Churchill, S. W.; Bernstein, M. (1977), "A Correlation Equation for Forced Convection from Gases and Liquids to a Circular Cylinder in Cross Flow", J. Heat Transfer, Trans. ASME 94: 300–306
- Incropera, F.P.,; DeWitt, D.P., Bergman, T.L., and Lavine, A.S. (2006). Fundamentals of Heat and Mass Transfer, 6th Ed.. Wiley. ISBN 978-0-471-45728-2. http://www.amazon.com/dp/0470055545.
- Tammet, Hannes; Kulmala, Markku (June), Simulating aerosol nucleation bursts in a coniferous forest, http://www.borenv.net/BER/pdfs/ber12/ber12-421.pdf, retrieved 10/07/2007
- Ramachandran Venkatesan; Scott Fogler (2004). "Comments on Analogies for Correlated Heat and Mass Transfer in Turbulent Flow". AIChE Journal 50 (7): 1623–1626. doi:10.1002/aic.10146.
- Martínez, Isidoro, Forced and Natural Convection, http://webserver.dmt.upm.es/~isidoro/bk3/c12/Forced%20and%20natural%20convection.pdf, retrieved 2011-11-30